Während es das Ziel der ANOVA oder MANOVA ist, den Einfluss kategorialer Variablen auf eine intervallskalierte zu ermitteln, sollen mit der linearen Regressionsanalyse die Einflüsse mehrerer unabhängiger Variablen (kategorial, ordinal oder intervallskaliert) un tersucht werden. Die lineare Regressionsanalyse gilt in der Anwendung bei StudentInnen und Ghostwritern für Statistik als eines der flexibelsten und am häufigsten genutzten Testverfahren, das in Bachelorarbeiten genauso Anwendung findet wie in Master- oder Doktorarbeiten und einfach in SPSS, Stata und RStudio zu berechnen ist. Im Unterschied zu anderen, bisher diskutierten Verfahren wie der Korrelationsanalyse ist es mit der linearen Regression relativ gut möglich, Ursache-Wirkungs-Zuschreibungen zu analysieren und das Verhalten der abhängigen Variable in Abhängigkeit von ihren Prädiktoren zu modellieren.
Auch wenn es sich bei der linearen Regression um ein verbreitetes Verfahren handelt, gibt es auch hier einige Voraussetzungen zu beachten, die gerade für die Masterarbeit und Dissertation von StudentInnen wichtig sind. Je nach verwendeter Statistiksoftware ist die Über prüfung dieser Voraussetzungen in SPSS, Stata oder RStudio nicht immer trivial.
Da sich mit der linearen Regression bereits einige Statistiklehrbücher befassen, sind nach folgend nur die grundlegendsten Voraussetzungen vereinfacht dargestellt:
Je nach Verletzung dieser und weiterer Voraussetzungen für die Anwendung der linearen Regression in SPSS, Stata oder RStudio kann es sein, dass das Verfahren an Aussagekraft einbüßt oder gar nicht mehr interpretierbar wird, weil beispielsweise die Voraussetzungen für den t-Test auf Mittelwertunterschiede verletzt sind.
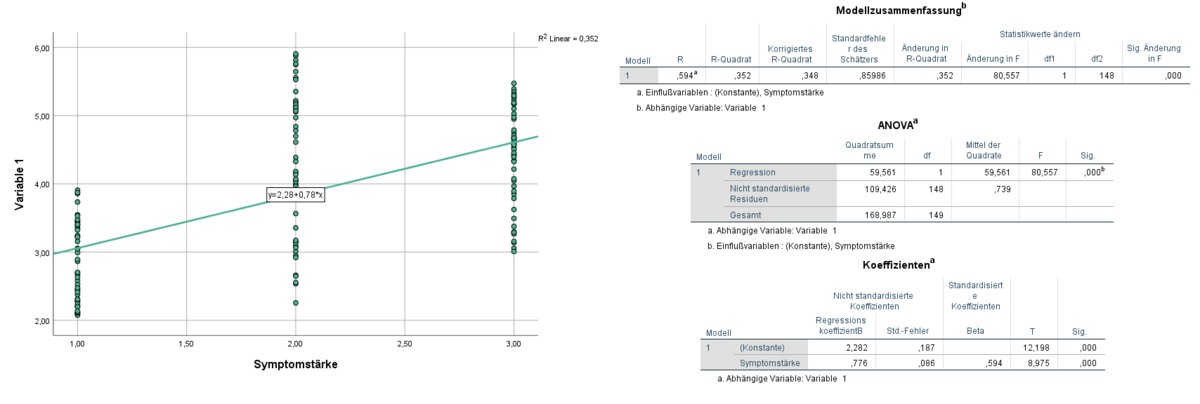
Grundsätzlich ist es das Ziel jeder linearen Regressionsanalyse, aus einer Wolke aus Datenpunkten diejenige Regressionsgerade zu berechnen, welche den geringsten mittleren Abstand zu jedem einzelnen Messpunkt aufweist. Die Ausgabe, die von SPSS, Stata oder RStudio generiert wird, sieht dabei immer etwas unterschiedlich aus, weshalb die Anwendung der linearen Regression kurz anhand von SPSS dargestellt wird.
Anhand der unten dargestellten SPSS-Auswertung ist erkennbar, dass mit dem berechneten linearen Regressionsmodell eine unabhängige Variable (Symptomstärke) als signifikanter Prädiktor von Variable 1 identifiziert werden konnte. Dies ist in der zugehörigen ANOVA-Statistik ersichtlich. Über die Koeffizientenstatistik können StudentInnen und Ghostwriter für Statistik ablesen, dass Variable 1 umso größer wird, je stärker die Symptome ausgeprägt sind. Außerdem ist die Anpassungsgüte des Modells angegeben, die SPSS mit 0,352 berechnet hat, was bedeutet, dass 35,2 % der Varianz von Variable 1 über die unabhängige Variable ‚Symptomstärke‘ erklärt werden können.
Trotz oder gerade wegen des Umstands, dass lineare Regressionsanalysen so weite Verbreitung gefunden haben, kommt es immer wieder vor, dass die Voraussetzungsprü fung für dieses Verfahren von StudentInnen und Ghostwritern für Statistik unterschätzt wird. Mitunter wirken sogar BetreuerInnen von Bachelor-, Master- oder Doktorarbeiten überfordert vom Anforderungsreichtum des Verfahrens, zudem lassen mit einer linearen Regressionsanalyse mehrere Seiten des Ergebnisteils füllen, wenn alle Voraussetzungen berücksichtigt werden. Dieser Umstand macht das Verfahren gerade bei Masterarbeiten und Dissertationen anspruchsvoll für die StudentInnen, denn die BetreuerInnen wissen oft um dessen Anfälligkeit – gerade in der Verteidigung. Ghost&Write möchte Sie deshalb unterstützen, indem wir die Regressionsanalyse durchführen oder Ihnen bei der eigenen Durchführung beratend zur Seite stehen.
